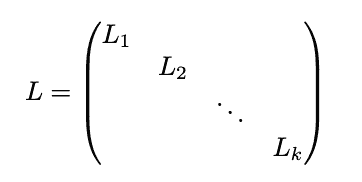
Intro to spectral graph theory
September 02, 2021 3 min read
Spectral graph theory is an amazing connection between linear algebra and graph theory, which takes inspiration from multivariate calculus and Riemannian geometry. In particular, it finds applications in machine learning for data clustering and in bioinformatics for finding connected components in graphs, e.g. protein domains.
A motivational example
Suppose that you are given a graph, and you need to find the number of connected components in it. Moreover, the problem can be fuzzy, i.e. formulated in terms of finding dense sub-graphs of a graph. For instance, you might have a 3D-structure of a protein, where graph vertices correspond to C-alpha atoms of amino acid residues, and edges might connect nearby pairs of C-alpha atoms. You might want to find dense sub-graphs of C-alpha atoms, called protein domains.
It turns out, that linear-algebraic approach to graphs might lead to amazing results.
Suppose that you have an undirected graph with weights on its edges.
Let us define its adjacency matrix A:
,
where each element of represents the weight of the edge i -> j.
As the graph is assumed undirected, the adjacency matrix is symmetric; moreover, we’ll have it positively definite.
Let us also consider a diagonal degree matrix D:
,
where is the sum of weights of all edges, leading to/from the vertex i.
Turns out, the difference between degree and adjacency matrices, the matrix has some amazing properties. For instance, the algebraic multiplicity of its eigenvalue 0 corresponds to the number of connected components in the graph! This matrix L is called graph Laplacian.
Here is a nice example from wikipedia (here no weights on edges are specified, so if an edge exists, we assume its weight 1, if it doesn’t - 0):
If you recall Laplacian operator in multivariate calculus/physics, it is actually the same concept, the Laplacian matrix is just its discrete analogue. The wonderful properties of Laplacian matrix become more obvious from this analogy, so I’ll take a detour to explain the notion of Laplacian in multivariate calculus.
Laplacian in multivariate calculus
The intuitive meaning of Laplacian is not immediately obvious from its definition.
To appreciate its usefulness, you need to understand Gauss-Ostrogradsky divergence theorem first.
TODO: sum of neighbors
TODO: connection to hessian - Laplacian is a trace of Hessian, divergence is a trace of Jacobian
Connection between Laplacian operator and graph Laplacian/normalized graph Laplacian
TODO: difference between the average of function over the neighbours, and the value of function at the point
Properties of graph Laplacian
TODO: connection to Rayleigh quotient
Discrete Laplace operator
A fun fact: there exists yet another discrete version of Laplacian, a Discrete Laplace Operator, which is often used as a convolution filter in computer vision to detect edges in images.
It is a matrix of the following structure in 2D case:
, where is the size of a step in the context of finite difference method.
Try applying it to a brick wall as a good example - you’ll see that a solid brick will be zeroed (as its margin doesn’t differ from the solid part), but its edge, where it touches the concrete, will be highlighted, as there is a colour difference.
References
- https://people.csail.mit.edu/dsontag/courses/ml14/notes/Luxburg07_tutorial_spectral_clustering.pdf - a great tutorial on spectral graph theory
- http://www.math.ucsd.edu/~fan/research/cb/ch1.pdf - a popular textbook by Fan Chung on spectral graph theory
- https://math.stackexchange.com/questions/50274/intuitive-interpretation-of-the-laplacian - interpretation of Laplacian in multivariate calculus
- https://math.stackexchange.com/questions/18945/understanding-the-properties-and-use-of-the-laplacian-matrix-and-its-norm - answer by Qiaochu Yuan and others
- https://qchu.wordpress.com/2011/01/02/the-schrodinger-equation-on-a-finite-graph/ - connections with quantum mechanics
- https://math.stackexchange.com/questions/4089508/intuition-of-the-connection-between-the-graph-laplacian-and-the-laplace-operator - awesome explanation of connection of two Laplacians
- https://mathoverflow.net/questions/54986/why-is-the-laplacian-ubiquitous - answer by Terry Tao and others about ubiquity of laplacian
- https://www.youtube.com/watch?v=uxsDKhZHDcc - lectures on spectral clustering by Jure Lescovec

Written by Boris Burkov who lives in Moscow, Russia, loves to take part in development of cutting-edge technologies, reflects on how the world works and admires the giants of the past. You can follow me in Telegram

