BorisBurkov.net
my photo
Written by Boris Burkov who lives in Moscow, Russia, loves to take part in development of cutting-edge technologies, reflects on how the world works and admires the giants of the past.

You can follow me in Telegram

Categories

biomed 9business 7economy 7history 7how-life-works 13math 34music 1people 11programming 27
cover

Lasso regression implementation analysis

February 15, 2022 14 min read

Lasso regression algorithm implementation is not as trivial as it might seem. In this post I investigate the exact algorithm, implemented in Scikit-learn, as well as its later improvements.

The computational implementation of Lasso regression/ElasticNet regression algorithms in Scikit-learn package is done via coordinate descent method. As I had to re-implement a similar L1 regularization method for a different problem of large dimensionality, I decided to study L1 regularization implementation from Scikit-learn in detail.

Scikit-learn Lasso regression implementation

Consider the problem we aim to solve. We need to minimize the weighted sum of 2 terms: first term is the sum of squares of regression residues, second term is L1 norm of regression weights with some hyperparameter α\alpha:

f(w)=(y−Xw)2⏟sum of squares of regression residues+α∣∣w∣∣1⏟L1-norm of regression weights=∑i=1n(yi−∑j=1pwjXi,j)2⏟sum of squares of regression residues+α∣∣w∣∣1⏟L1-norm of regression weights→minf({\bf w}) = \underbrace{ ({\bf y} - X {\bf w})^2}_{\text{sum of squares of regression residues}} + \underbrace{\alpha ||{\bf w}||_{1}}_\text{L1-norm of regression weights} = \underbrace{ \sum \limits_{i=1}^{n} (y_i - \sum \limits_{j=1}^{p} w_j X_{i,j})^2}_{\text{sum of squares of regression residues}} + \underbrace{\alpha ||{\bf w}||_{1}}_{ \text{L1-norm of regression weights} } \to min

Luckily, f(w)f({\bf w}) function is tractable, so it is easy to perform exact calculations of its gradient, hessian etc.

Thus, we don’t have to rely on the savvy techniques from numeric optimization theory, such as line search, Wolfe conditions etc.

Scikit-learn implementation of Lasso/ElasticNet uses a simple iterative strategy to find the optimum of this function. It iteratively does coordinate-wise descent. I.e. at each step of the algorithm it considers each of the coordinates wiw_i one by one and minimizes f(w)f({\bf w}) relative to the coorindate wiw_i. At the end of each step it checks, whether the largest update among the regression weights max⁡i∣wi−wi−1∣\max_i |w_{i}-w_{i-1}| was larger than a certain tolerance parameter. If not, it finally checks the duality gap between the solution of primal and dual Lagrange problems for Lasso (more on the dual problem later), and if the gap is small enough, returns the weights and stops successfully. If dual gap has not converged, although regression weights almost stopped decreasing, it emits a warning.

Coordinate descent

At each step of our loop we will optimize each of the regression weights individually.

In order to do that, we will be calculating the partial derivative of the optimized function by each individual weight:

∂f∂wk=2⋅∑i=1n(yi−∑j=1pwjXi,j)⋅(−Xi,k)+α∂∣wk∣∂wk\frac{\partial f}{\partial w_k} = 2 \cdot \sum \limits_{i=1}^{n} (y_i - \sum \limits_{j=1}^{p} w_j X_{i,j}) \cdot (-X_{i,k}) + \alpha \frac{\partial|w_k|}{\partial w_k}

To find the new optimal value of weight wiw_i we will be looking for a point, where our function takes the minimum value, i.e. its partial derivative on wiw_i equals 0:

∂f∂wk=0:\frac{\partial f}{\partial w_k} = 0:

∑i=1n(yi−∑j=1pwjXi,j)⋅(−Xi,k)+α2⋅∂∣wk∣∂wk=0\sum \limits_{i=1}^{n} (y_i - \sum \limits_{j=1}^{p} w_j X_{i,j}) \cdot (-X_{i,k}) + \frac{\alpha}{2} \cdot \frac{\partial|w_k|}{\partial w_k} = 0

∑i=1n(yiXi,k−∑j=1pwjXi,jXi,k)=α2⋅∂∣wk∣∂wk\sum \limits_{i=1}^{n} (y_i X_{i,k} - \sum \limits_{j=1}^{p} w_j X_{i,j} X_{i,k}) = \frac{\alpha}{2} \cdot \frac{\partial|w_k|}{\partial w_k}

∑i=1n(yiXi,k−∑j≠kwjXi,jXi,k)−∑i=1nwkXi,k2=α2⋅∂∣wk∣∂wk\sum \limits_{i=1}^{n} (y_i X_{i,k} - \sum \limits_{j \ne k} w_j X_{i,j} X_{i,k}) - \sum \limits_{i=1}^{n} w_k X_{i,k}^2 = \frac{\alpha}{2} \cdot \frac{\partial|w_k|}{\partial w_k}

wk⋅∑i=1nXi,k2=∑i=1n(yiXi,k−∑j≠kwjXi,jXi,k)−α2⋅∂∣wk∣∂wkw_k \cdot \sum \limits_{i=1}^{n} X_{i,k}^2 = \sum \limits_{i=1}^{n} (y_i X_{i,k} - \sum \limits_{j \ne k} w_j X_{i,j} X_{i,k}) - \frac{\alpha}{2} \cdot \frac{\partial|w_k|}{\partial w_k}

wk=(∑i=1nXi,k(yi−∑j≠kwjXi,j)−α2⋅∂∣wk∣∂wk)/(∑i=1nXi,k2)w_k = (\sum \limits_{i=1}^{n} X_{i,k} (y_i - \sum \limits_{j \ne k} w_j X_{i,j}) - \frac{\alpha}{2} \cdot \frac{\partial|w_k|}{\partial w_k}) / (\sum \limits_{i=1}^{n} X_{i,k}^2)

To write this result in a compact vector/matrix form, denote the vector of regression residues R=y−Xw+wkXk{\bf R} = {\bf y} - X {\bf w} + w_k {\bf X_k},

where Xk=(X1,kX2,k...Xn,k){\bf X_k} = \begin{pmatrix} X_{1,k} \\ X_{2,k} \\ ... \\ X_{n,k} \end{pmatrix} is the k-th column of matrix XX.

Then we can re-write in vector form:

wk=(⟨R,Xk⟩−α2⋅∂∣wk∣∂wk)/∣∣Xk∣∣22w_k = (\langle {\bf R}, {\bf X_k} \rangle - \frac{\alpha}{2} \cdot \frac{\partial|w_k|}{\partial w_k}) / || {\bf X_k} ||_2^2.

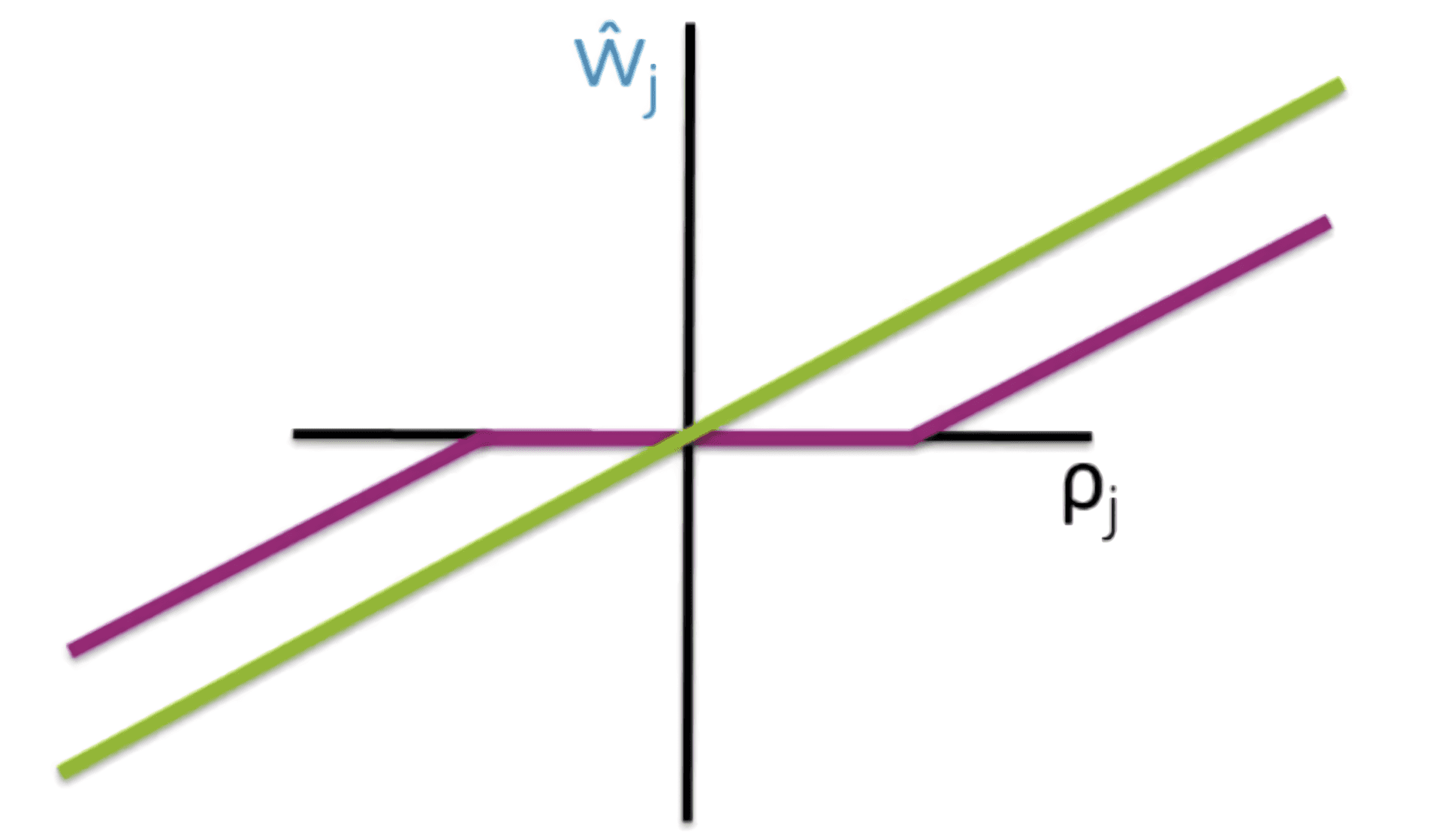
Subgradient

Now, we should focus on the derivative of L1 regularization term: ∂∣wk∣∂wk\frac{\partial|w_k|}{\partial w_k}.

For wk≠0w_k \ne 0 it is trivial: ∂∣wk∣wk=sign(wk)\frac{\partial|w_k|}{w_k} = sign(w_k).

However, it is undefined for wk=0w_k = 0, and we cannot ignore this case, as the whole purpose of L1 regularization is to keep most of our regression weights wkw_k equal to 0.

∂∣wk∣∂wk={1,wk>0−1,wk<0undefined,wk=0\frac{\partial |w_k|}{\partial w_k} = \begin{cases} 1, w_k > 0 \\ -1, w_k < 0 \\ \text{undefined}, w_k = 0 \end{cases}

The workaround from this situation is to replace the exact gradient with subgradient, which is a function less than or equal to the gradient in every point.

sub∂f∂wk=⟨R,Xk⟩−α2⋅sub∂∣wk∣∂wk−∣∣Xk∣∣22⋅wk⏟0=0  ⟹  sub∂∣wk∣∂wk=⟨R,Xk⟩/α2sub \frac{\partial f}{\partial w_k} = \langle {\bf R}, {\bf X_k} \rangle - \frac{\alpha}{2} \cdot sub \frac{\partial|w_k|}{\partial w_k} - \underbrace{ || {\bf X_k} ||_2^2 \cdot w_k}_\text{0} = 0 \implies sub \frac{\partial|w_k|}{\partial w_k} = \langle {\bf R}, {\bf X_k} \rangle / \frac{\alpha}{2}

Now, the allowed values of the subgradient are bounded by the derivatives at wk=0+w_k = 0_+ and wk=0−w_k = 0_-:

−1≤sub∂∣wk∣∂wk≤1-1 \le sub \frac{\partial|w_k|}{\partial w_k} \le 1

Hence, substituting the subgradient from the formula above, we get:

−1≤⟨R,Xk⟩/α2≤1-1 \le \langle {\bf R}, {\bf X_k} \rangle / \frac{\alpha}{2} \le 1

−α2≤⟨R,Xk⟩≤α2-\frac{\alpha}{2} \le \langle {\bf R}, {\bf X_k} \rangle \le \frac{\alpha}{2}

Now, if we substitute the exact gradient in coordinate descent formula with subgradient, we get:

wk={(⟨R,Xk⟩−α2)/∣∣Xk∣∣22,wk>0  ⟺  ⟨R,Xk⟩>α2(⟨R,Xk⟩+α2)/∣∣Xk∣∣22,wk<0  ⟺  ⟨R,Xk⟩<−α20,−α2≤⟨R,Xk⟩≤α2w_k = \begin{cases} (\langle {\bf R}, {\bf X_k} \rangle - \frac{\alpha}{2} ) / || {\bf X_k} ||_2^2, w_k > 0 \iff \langle {\bf R}, {\bf X_k} \rangle > \frac{\alpha}{2} \\ (\langle {\bf R}, {\bf X_k} \rangle + \frac{\alpha}{2} ) / || {\bf X_k} ||_2^2, w_k < 0 \iff \langle {\bf R}, {\bf X_k} \rangle < -\frac{\alpha}{2} \\ 0, -\frac{\alpha}{2} \le \langle {\bf R}, {\bf X_k} \rangle \le \frac{\alpha}{2} \end{cases}

Stoppage criterion: Lasso dual problem and duality gap

Now, the stoppage criterion for the Lasso procedure is formulated in terms of pair of primal-dual optimisation problems.

While α\alpha is considered a parameter of the system, we introduce a variable substitution Xw−y=zX {\bf w} - {\bf y} = {\bf z}.

We present this variable substitution as a set of constraints for the optimisation problem and apply Lagrange multipliers to it:

L(w,Λ,z)=z2+α∣∣w∣∣1+ΛT(Xw−y−z)\mathcal{L}({\bf w}, {\bf \Lambda}, {\bf z}) = {\bf z}^2 + \alpha || {\bf w} ||_1 + {\bf \Lambda}^T (X {\bf w} - {\bf y} - {\bf z})

Lagrange dual problem is to find Λ∗=arg⁡max⁡Λinf⁡w,zL(w,Λ,z){\bf \Lambda^*} = \arg \max \limits_{\bf \Lambda} \inf \limits_{\bf w, z} \mathcal{L}({\bf w}, {\bf \Lambda}, {\bf z})

First, split our Lagrangian into 2 terms that we optimize independently:

L(w,Λ,z)=z2−ΛT(z+y)⏟Term 1: minimize in z+α∣∣w∣∣1+ΛTXw⏟Term 2: minimize in w\mathcal{L}({\bf w}, {\bf \Lambda}, {\bf z}) = \underbrace{{\bf z}^2 - {\bf \Lambda}^T ({\bf z} + {\bf y} )}_\text{Term 1: minimize in {\bf z}} + \underbrace{\alpha || {\bf w} ||_1 + {\bf \Lambda}^T X {\bf w}}_\text{Term 2: minimize in {\bf w}}

Term 1 analysis

Let us take the partial derivatives of term 1 in ziz_i:

∂(z2−ΛT(z+y))∂zi=2zi−Λi=0\frac{\partial ({\bf z}^2 - {\bf \Lambda}^T ({\bf z} + {\bf y}))}{\partial z_i} = 2z_i - \Lambda_i = 0, and zi=Λi2z_i = \frac{\Lambda_i}{2}

Substituting this back into term 1, we get:

min⁡zT1=14ΛTΛ−214ΛTΛ−ΛTy=14ΛTΛ−ΛTy\min \limits_{\bf z} T_1 = \frac{1}{4} {\bf \Lambda}^T {\bf \Lambda} - 2 \frac{1}{4} {\bf \Lambda}^T {\bf \Lambda} - {\bf \Lambda}^T {\bf y} = \frac{1}{4} {\bf \Lambda}^T {\bf \Lambda} - {\bf \Lambda}^T {\bf y}

Term 2 analysis

Let us take the partial derivatives of term 2 in wiw_i:

∂(α∣∣w∣∣1+ΛTXw)∂wi=α⋅sign(wi)+{ΛTX}i=0\frac{\partial ({\alpha || {\bf w} ||_1 + {\bf \Lambda}^T X {\bf w})}}{\partial w_i} = \alpha \cdot sign(w_i) + \{{\bf \Lambda}^T X\}_i = 0

min⁡wiT2={0,∣{ΛTX}i∣≤α−∞,∣{ΛTX}i∣>α\min \limits_{w_i} T_{2} = \begin{cases} 0, |\{{\bf \Lambda}^T X\}_i| \le \alpha \\ -\infty, |\{{\bf \Lambda}^T X\}_i| > \alpha \end{cases}

(you can get {ΛTX}iwi\{{\bf \Lambda}^T X\}_i w_i term to be negative, and it will outgrow α⋅sign(wi)\alpha \cdot sign(w_i) if ∣{ΛTX}i∣>α|\{{\bf \Lambda}^T X\}_i| > \alpha)

Hence, if any of ii terms ∣{ΛTX}i∣>α|\{{\bf \Lambda}^T X\}_i| > \alpha, min⁡T2=−∞\min T_2 = -\infty, otherwise, min⁡T2=0\min T_2 = 0.

Taking the terms together and solving the Lagrange dual

The optimal value of Lagrangian, corresponding to the solution of this problem is:

inf⁡w,zL(Λ)={−14ΛTΛ−ΛTy,{∣XTΛ∣}i≤α−∞,otherwise\inf \limits_{\bf w, z} \mathcal{L}({\bf \Lambda}) = \begin{cases} -\frac{1}{4} {\bf \Lambda}^T {\bf \Lambda} - {\bf \Lambda}^T {\bf y}, \{|X^T {\bf \Lambda}|\}_i \le \alpha \\ -\infty, otherwise \end{cases}

So, we’ve come to a dual optimization problem: we need to achieve the maximum of dual function:

q(Λ)=−14ΛTΛ−ΛTyq({\bf \Lambda}) = -\frac{1}{4} {\bf \Lambda}^T {\bf \Lambda} - {\bf \Lambda}^T {\bf y},

given a set of inequality constraints {∣XTΛ∣}i≤α\{|X^T {\bf \Lambda}|\}_i \le \alpha (or, in an infinity-norm notation ∣∣XTΛ∣∣∞≤α||X^T {\bf \Lambda}||_{\infty} \le \alpha).

Optionally, we can subtract yTy{\bf y}^T {\bf y} to the q(Λ)q({\bf \Lambda}) function, as it does not affect the minimization, as this form is more convenient for geometric interpretation. This results in:

max⁡Λh(Λ)=∣∣Λ−y∣∣22\max \limits_{\bf \Lambda} h({\bf \Lambda}) = || \bf \Lambda - y ||_2^2, subject to ∣∣XTΛ∣∣∞≤α||X^T {\bf \Lambda}||_{\infty} \le \alpha

The problem is convex and by Slater’s condition if the solution of primal problem is feasible, the duality is strict.

Hence, duality gap converges to 0, and we can use it as a stoppage criterion in our Lasso problem.

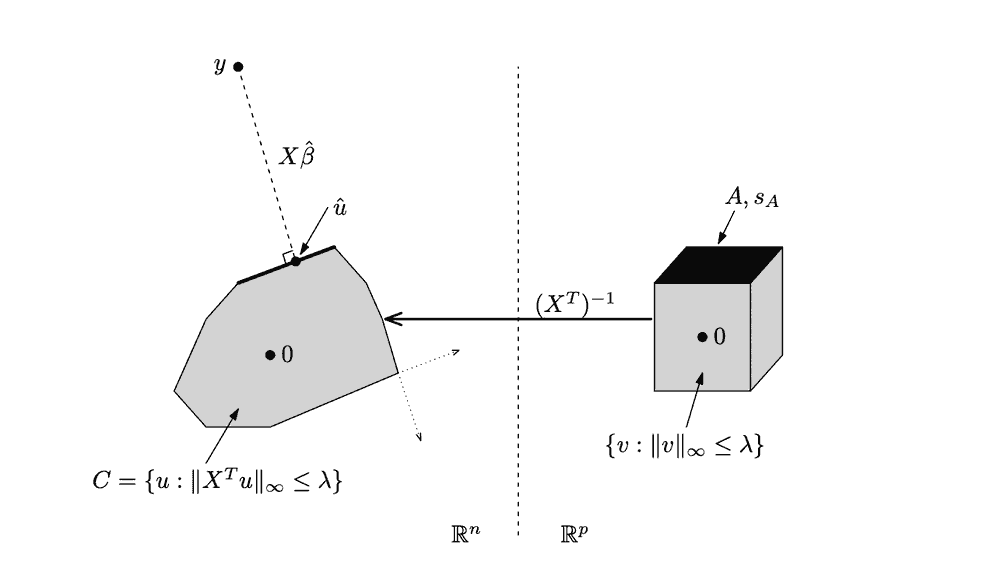
Geometric interpretation of Lagrange dual

The last form of Lasso dual max⁡Λh(Λ)=∣∣Λ−y∣∣22\max \limits_{\bf \Lambda} h({\bf \Lambda}) = || \bf \Lambda - y ||_2^2, subject to ∣∣XTΛ∣∣∞≤α||X^T {\bf \Lambda}||_{\infty} \le \alpha allows for a direct, beautiful and intuitive geometric interpretation, provided by Ryan Tibshirani (tutorial page 11, lecture 18 slides).

Lasso dual by Tibshirani

Right-hand side: Λ\bf \Lambda dual vectors with L∞L_\infty norm (here denoted vv) having each coordinate not greater than α\alpha (here denoted λ\lambda). Hence, those dual vectors form a cube in Rp\mathbb{R}^p space (where pp is the number of predictors).
Left-hand side: if we were to multiply those dual vectors by inverse of XTX^T matrix, we go back into the primal space Rn\mathbb{R}^n. In primal space the cube of valid dual vectors Λ\bf \Lambda (vv) is transformed into a convex polytope, where the image of each vector Λ\bf \Lambda (vv) is denoted uu. By solving the Lasso regression problem we find such a direction w\bf w that projection of the vector y\bf y onto this polytope along direction XwX {\bf w} is a specific vector uu, such that the length of the normal to this projection ∣∣Xw−y∣∣2|| X {\bf w} - \bf y ||_2 is minimal.

Alternatives: preconditioned conjugate gradients, quadratic programming, safe rules

TODO

References

Boris Burkov

Written by Boris Burkov who lives in Moscow, Russia, loves to take part in development of cutting-edge technologies, reflects on how the world works and admires the giants of the past. You can follow me in Telegram